澤崎郁¹

[1] 防災科学技術研究所

doi:10.1785/0120200365

Date: 2021-6-15

要旨

　 　　　　　　
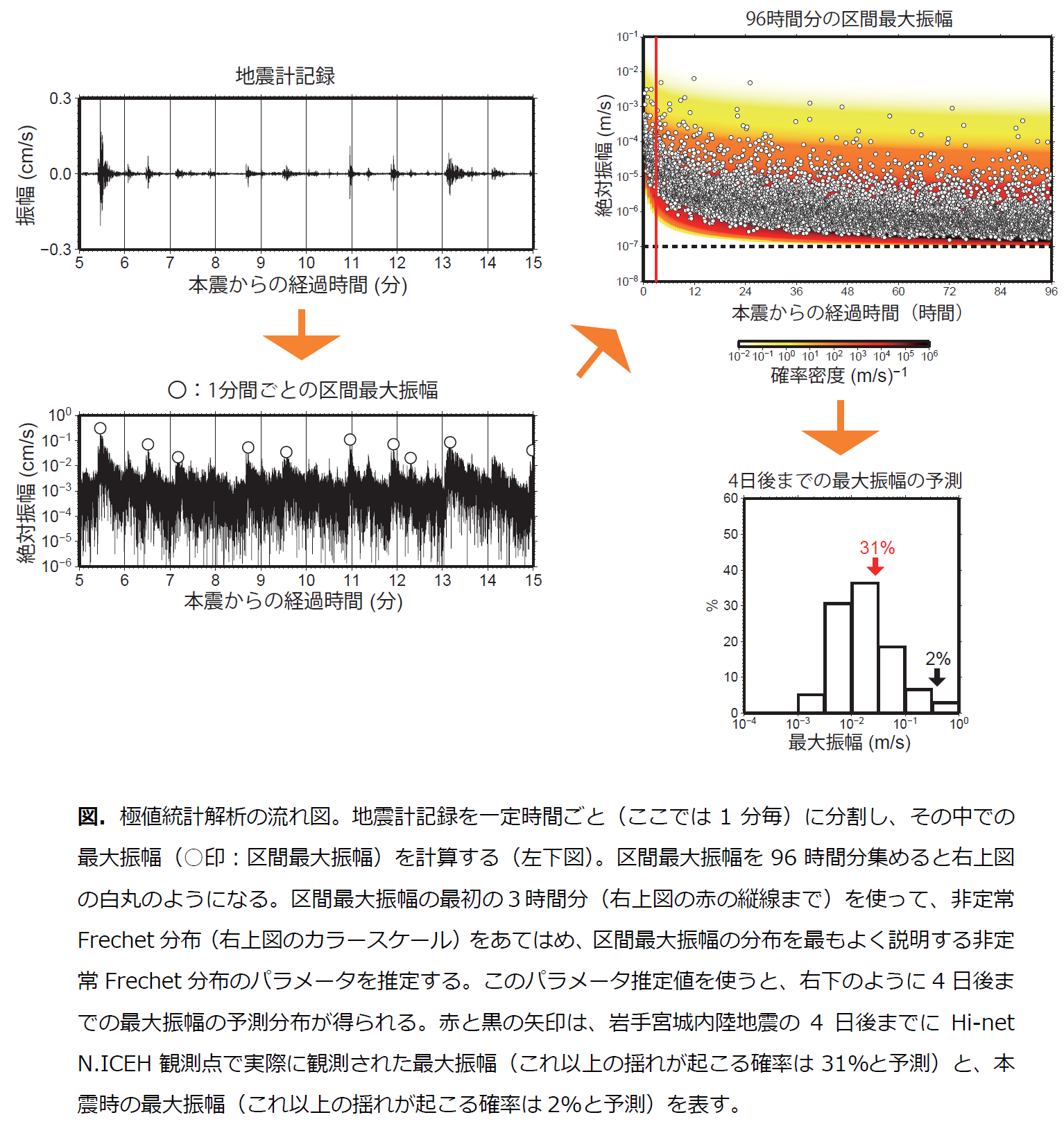
大地震の後には余震が活発に起こります。余震活動の推移を早く正確に予測できれば、発災後の避難や復旧活動を円滑に進める上で非常に有用となると考えられます。従来は、余震の発生頻度とマグニチュードがそれぞれ大森・宇津則（＊１）とグーテンベルク・リヒター則（＊２）にしたがうことを利用して、「マグニチュードOO以上の地震がOO日以内に起こる確率はOO％」という予測が行われてきました。しかし、大地震の直後には余震があまりにも多く起こるため、地震計記録上ではいくつもの余震による地震波が「重なり合って」記録されます（図参照）。地震波が重なり合う記録からは、地震の個数やマグニチュードを正確に読み取ることができなくなります。そのため、従来の手法は、地震波が重なり合わないくらいに地震の数が少なくなってから（おおむね１週間後以降）初めて適用できるものであり、最も重要な大地震直後の時間帯では実用的に使える手法ではありませんでした。
　本研究では、地震計記録を一定時間ごとに区切り、それぞれの時間帯での最大振幅（区間最大振幅。図参照）がどのような統計則にしたがうかを、極値統計（＊３）という理論に基づき検討しました。その結果、区間最大振幅が「非定常Frechet分布」という確率分布にしたがうことが分かりました。この確率分布を用いて2008年岩手・宮城内陸地震の発生後3時間以内の地震計記録を解析し、「最大振幅OO以上の揺れが４日以内に起こる確率はOO％」という予測を行った結果、4日以内に生じた実際の最大の揺れを、実用上そん色ない精度で予測することができました。従来法では「マグニチュード」を予測していましたが、新手法ではより被害に直結する「揺れの強さ」を観測地点ごとに予測できるようになりました。
　この手法では余震だけではなく観測地点ごとの「普段の地震活動」を把握することができるため、大地震が起こった後の余震活動が「普段の何倍くらい活発か」などの情報を提供できると考えられます。また、最大振幅だけではなく震度の予測も可能と考えられます。今後は、様々なタイプの過去の地震にこの手法を適用し、その適用範囲の検証を進める予定です。 　　　　　

掲載情報

本成果は，2021年6月15日に米国地震学会発行の学術誌「Bulletin of the Seismological Society of America」にオンライン掲載されました．

論文：Sawazaki, K. (2021) Early forecast of maximum amplitude due to aftershocks by applying extreme value statistics to a single continuous seismogram, Bull. Seism. Soc. Am., 111(5). 2825-2845 DOI:10.1785/0120200365. 　　　　　　
　　　　　

備考

本研究はJSPS科研費JP17K14385の助成を受けたものです。解析には、防災科研Hi-net、KiK-netのデータを用いました。 　　　　　　
　　　　　

用語の説明

※1　大森・宇津則（または改良大森則） 　　　　　　
本震後の経過時間と余震の発生頻度との関係を表す経験則の一つ。経過時間をtとすると、発生頻度はt^p分の1に比例する。pの値は1よりやや大きい場合が多い。

※2　グーテンベルク・リヒター則 　　　　　　
地震の規模（マグニチュード）と発生頻度との関係を表す経験則の一つ。マグニチュードが1大きくなると発生頻度が10^b分の1に下がる。bの値には地域性があり時間変化もするが、概ね1程度である場合が多い。

※3　極値統計学 　　　　　　
大地震や集中豪雨など、めったに起こらないが起こると重大な結果をもたらす現象を扱う際には、ある期間の中での最大（または最小）のイベントがどのような確率分布にしたがうかが重要となる。このような最大値（または最小値）がしたがう統計則を扱う学問を極値統計学という。